
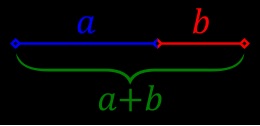
Le nombre d’or (ou section dorée, proportion dorée, ou encore divine proportion) est une proportion, définie initialement en géométrie comme l’unique rapport a/b entre deux longueurs a et b telles que le rapport de la somme a + b des deux longueurs sur la plus grande (a) soit égal à celui de la plus grande (a) sur la plus petite (b) c’est-à-dire lorsque :
Le découpage d’un segment en deux longueurs vérifiant cette propriété est appelé par Euclide découpage en « extrême et moyenne raison ». Le nombre d’or est maintenant souvent désigné par la lettre φ (phi), et il est lié à l’angle d’or.
Ce nombre irrationnel est l’unique solution positive de l’équation x2 = x + 1. Il vaut :
Il intervient dans la construction du pentagone régulier. Ses propriétés algébriques le lient à la suite de Fibonacci et au corps quadratique ℚ(√5). Le nombre d’or s’observe aussi dans la nature (quelques phyllotaxies, par exemple chez les capitules du tournesol, pavage de Penrose de quasi-cristaux) ou dans quelques œuvres et monuments (architecture de Le Corbusier, musique de Xenakis, peinture de Dalí).
Les dimensions de ma création en 3D de PHI est de :
L=17,4 ; l=18 ; H=6 cm.
Tarif disponible dans la rubrique, services et prestations.


